Contenidos
En este curso de Cálculo 1 de la Facultad de Ciencias Económicas, trataremos diferentes temas, ajustando estos al los temas tratados en el curso de la Facultad.
Los temas a ser tratados en el curso son los siguientes:
Recta Costo Ingreso Utlidad, Función Inversa, Derivadas, Polinomio de Taylor, Integrales definidas y Primitivvas, Teorema Fundamental del cálculo, Integrles Impropias y Serias
Para repasar conceptos básicos para este curso te recomendamos visitar nuestro canal de Youtube haciendo clic en el siguiente enlace
Para acceder a los vídeos de resolución del curso debes adquirir el mismo en PROFEonline, para ampliar información comunícate por WhatsApp al +598 96 146 694
Función Lineal – Costo Ingreso Utilidad – Oferta Demanda
EJERCICIO 1
Ejercicio de las funciones Costo, Ingresos y Utilidad
EJERCICIO 2
Una empresa produce un artículo cuya oferta es una función lineal; donde
se ofrecen las cantidades 120 y 160 para los precios de 1 y 2 dólares por unidad respectivamente.
La demanda viene dada por d(p) = 50p2 − 500p + 1250. Encontrar el punto de equilibrio (el valor de p para el cual la oferta coincide con la demanda).
Limites y Continuidad
EJERCICIO 3
CÁLCULO de LÍMITES de Funciones Partidas o Función Definida a Trozos
EJERCICIO 4
Calcular los límites de las siguientes funciones en los puntos indicados:

EJERCICIO 5
En este ejercicio se pide Investigar en qué puntos son continuas las funciones dadas.

EJERCICIO 6
Se considera la siguientes funcione de R en R:

Hallar las constantes a y b sabiendo que f es continua en todo R.
Derivadas
Definición de DERIVADA

En el ejercicio siguiente debemos calcular la derivada de una constante K; es decir que para todo valor de x la función siempre vale K:
Entonces f(x)=K
Por lo tanto f(x+h)= K y f(x)= K por lo que el planteo me quedaría

es importante destacar que esta división es 0 dividido algo que tiende a 0 y por lo tanto el divisor no es 0 absoluto y el numerador sí.
Entonces concluimos que si K es una constante:

Ejercicio 7 – Definición de Derivadas
En este video veremos la derivada por definición de una función
Además calcularemos la Derivada de f(x)=X por definición
Ejercicio 8 – Derivadas por Definición de X2
Calcular la derivada de la función f(x)=X2 aplicando la definición de derivada.
Ejercicio 9 – Función exponencial
En este caso calcularemos la Derivada por definición de la función exponencial
Ejercicio 10 – Derivadas por Definición de la función Logaritmo
Determinar la derivada de la función F(x)=L(x) calculando el límite que define a la derivada
Cálculo Práctico de Derivadas
Aquí puedes descargar las tabla de Derivadas para resolver los próximos ejercicios
Ejercicio 11 – Derivadas por tablas
En este conjunto de ejercicios trataremos de ver de manera fácil y rápida cómo se utiliza la tabla de derivadas para lograr derivar una función en forma práctica y obtener rápidamente la solución del ejercicio planteado.
Ejercicio 12 – Derivadas por tablas
13 Ejercicio – Cálculo práctico de Derivadas por tablas
Ejercicio 14 – Derivar una Multiplicación
En este caso estaremos calculando la derivada de una multiplicación aplicando la fórmula correspondiente y las tablas de derivadas.
Ejercicio 15 – Derivar una División
Calculo de la Derivada de una División
Regla de la Cadena
Ejercicio 16
Regla de la cadena
Ejercicio 17
Ejercicio 18
Ejercicios de Derivadas de funciones compuestas con Logaritmos (Reglade la Cadena)
Recta Tangente
19 EJERCICIO
Calcular la tangente de la función f(x)=L|X| en el punto X=e
Función Inversa
20 EJERCICIO
Polinomio de Taylor
EJERCICIO 21
22 EJERCICIO
23 EJERCICIO
EJERCICIO 24
25 EJERCICIO
Integrales
Integrales de Funciones por Intervalos
26 EJERCICIO
Integrales Propiedades
27 EJERCICIO
Cálculo de Primitivas
28 EJERCICIO
29 EJERCICIO
Barrow – Cálculo Integral
EJERCICIO 30
Área entre 2 funciones
EJERCICIO 31
32 EJERCICIO
EJERCICIO 33
Integración por Partes
Teorema de Integración por Partes
EJERCICIO 34
Integrales por Sustitución
EJERCICIO 35
EJERCICIO 36
Integrales por Fracciones Simples
CÁLCULO de INTEGRALES por Fracciones parciales
En el cálculo de integrales de funciones las cuales son cocientes de polinomios de la forma siguiente:
debemos comparar los grados de ambos polinomios:
Pueden presentarse dos casos:
- Si el grado del numerador P(x) es mayor o igual que el grado del denominador D(x); primero debemos dividir los polinomios obteniendo un cociente Q(x) y un resto R(x) y planteamos lo siguiente;
donde en esta última integral planteamos fracciones simples
- Si el grado del numerador P(x) es menor que el grado del denominador D(x); entonces aplicamos directamente el método de fracciones simples.
Método de Separación en Fracciones Simples
Separar en fracciones simples un cociente de polinomios consiste en lo siguiente:
vamos a realizar los siguientes pasos
Calculamos todas las raíces del divisor D(x) y planteamos su descomposición factorial como hemos aprendido en años anteriores. Pueden suceder tres casos diferentes:
- Todas las raíces son simples entonces el polinomio D(x) nos queda
y entonces se plantea lo siguiente:
y calculamos las constantes A, B . . . por diferentes métodos matemáticos que veremos en los ejercicios.
- Existen raíces múltiples; por cada grado de multiplicidad agregamos un término
- Raíz doble queda
- Si es Raíz triple queda
- Raíz doble queda
- Si existen raíces imaginarias nos queda de la forma siguiente:
Ejemplo Resuelto de una Integral por fracciones simples

Si observamos el grado del polinomio del numerador es menor que el grado del denominador; por lo tanto separamos en fracciones simples:

Ahora vamos a calcular las constantes A y B, damos valores a x en la igualdad anterior.
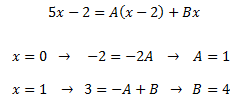
Posteriormente podemos escribir la integral como una suma; entonces aplicando propiedades, lo podemos expresar como una suma de integrales:

EJERCICIO 37
Integrales Impropias
Introducción al cálculo de Integrales Impropias de Primera Especie, características y procedimiento de cálculo de las mismas
Ejercicio 38
Ejercicio 39
Criterios de comparación para la clasificación de integrales impropias
Ejercicio 40
Criterio de la armónica
Ejercicio 41
Criterio de comparación
Ejercicio 42
Criterio de comparación por paso al límite
Ejercicio 43
Criterio del equivalente
